CS231n 笔记
一 图像分类:KNN与线性分类器
1 KNN算法基本原理
KNN(K Nearest Neighbors)是当预测一个新的值x时, 根据它距离最近的k个点是什么类别来判断x属于哪个类别。——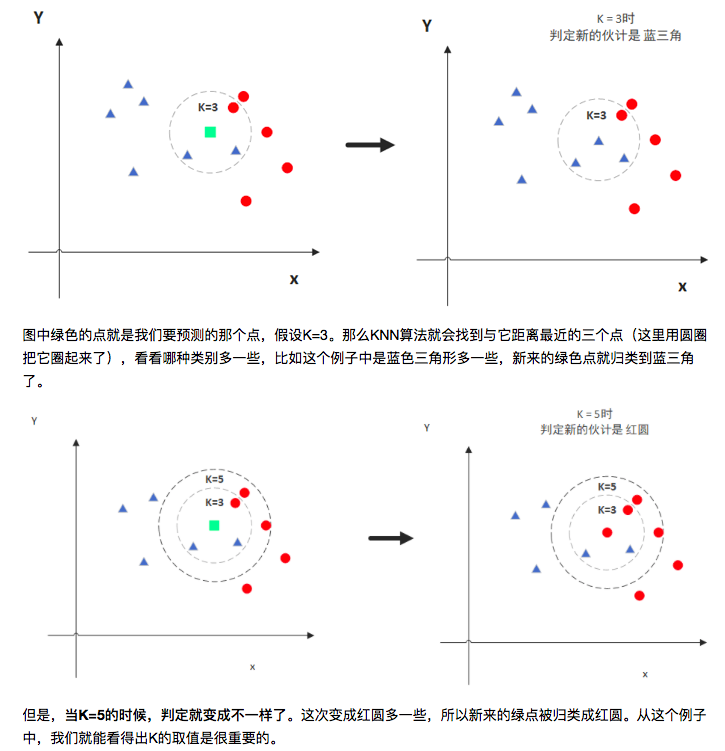
注意:K值的选取和点距离的计算
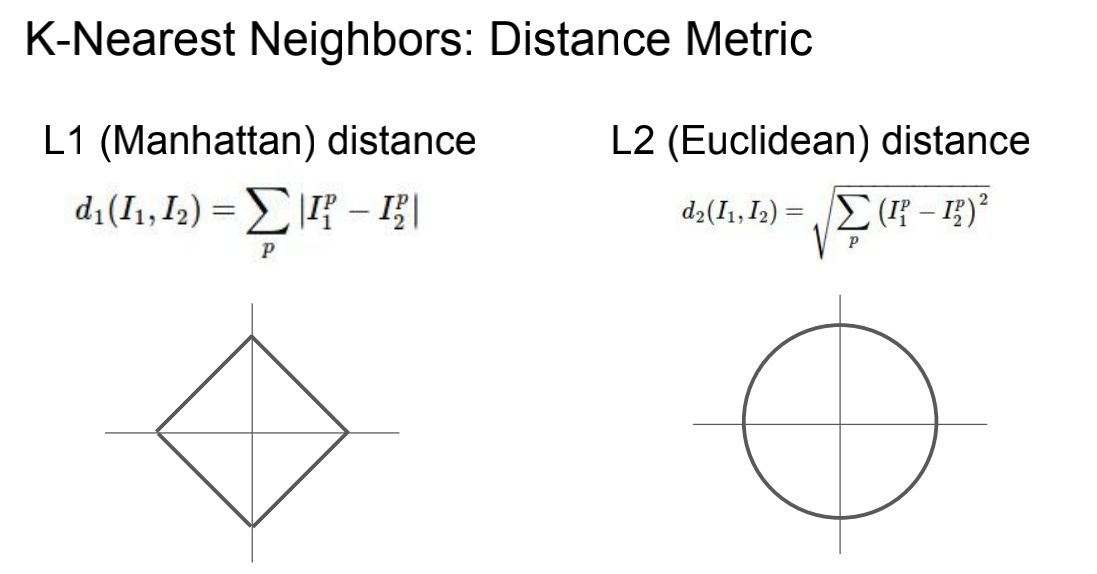
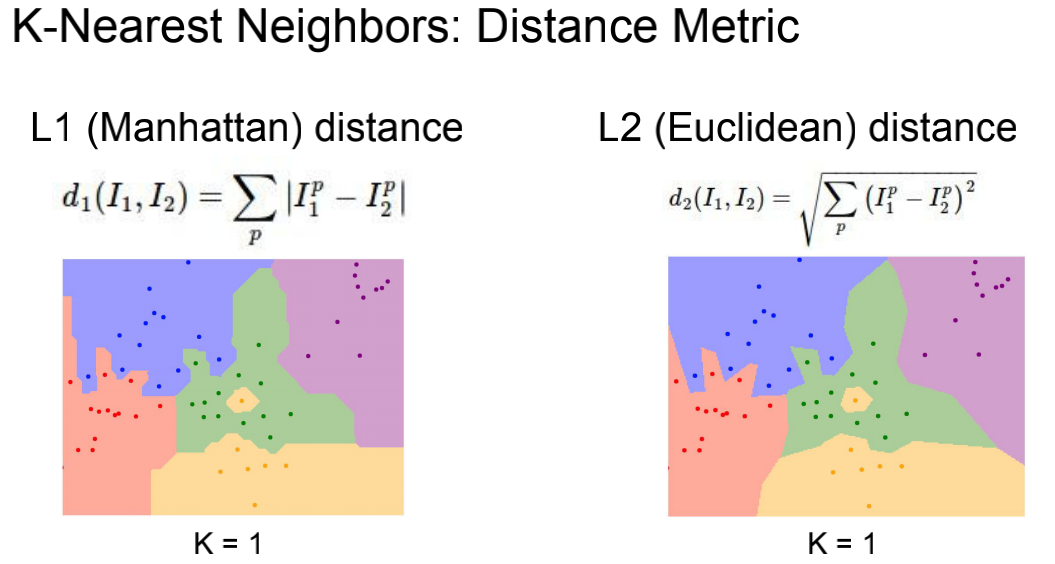
1.1 距离的计算
1.2 值的选取
通过交叉验证(将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据),从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的方差,最终找到一个比较合适的K值。——找到一个临界值。
1.3 KNN的特点
KNN是一种算法模型。
非参意味着这个模型不会对数据做出任何的假设,与之相对的是线性回归(我们总会假设线性回归是一条直线)。也就是说KNN建立的模型结构是根据数据来决定的,这也比较符合现实的情况,毕竟在现实中的情况往往与理论上的假设是不相符的。
惰性又是什么意思呢?想想看,同样是分类算法,逻辑回归需要先对数据进行大量训练(tranning),最后才会得到一个算法模型。而KNN算法却不需要,它没有明确的训练数据的过程,或者说这个过程很快。
KNN算法优点
- 简单易用,相比其他算法,KNN算是比较简洁明了的算法。即使没有很高的数学基础也能搞清楚它的原理。
- 模型训练时间快,上面说到KNN算法是惰性的,这里也就不再过多讲述。
- 预测效果好。
- 对异常值不敏感。
KNN算法缺点
- 对内存要求较高,因为该算法存储了所有训练数据
- 预测阶段可能很慢
- 对不相关的功能和数据规模敏感
总结
KNN是将不同图片中每个像素进行比较,差值最小即相似;超参数K意味着分类时取决附近K个值的分类。
二、线性分类、损失函数与最优化
2.1 线性分类
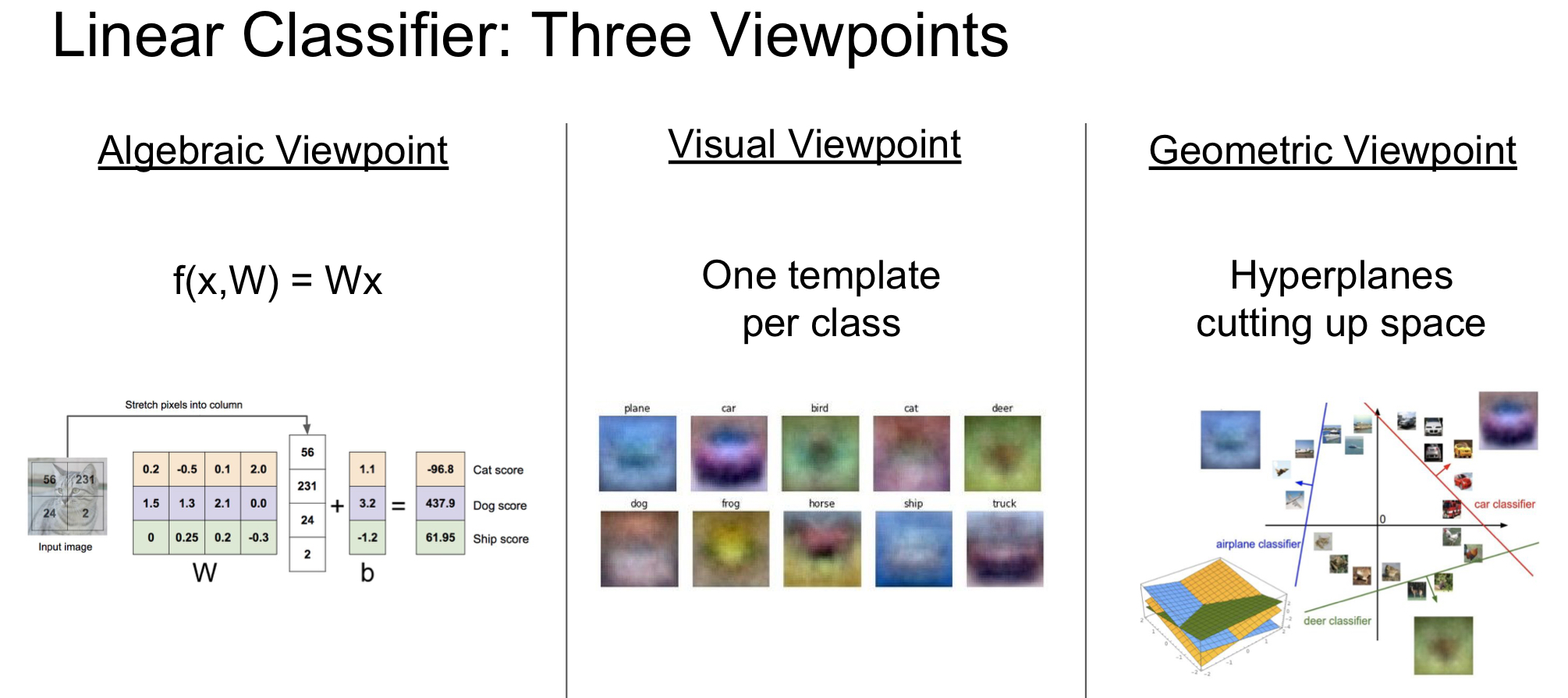
(1)线性分类由单层感知机可分类;非线性分类需要多层感知机。
如图一:线性映射(从图像到标签分值的参数化映射):$f(x_i,W,b)=Wx_i+b$
PS:参数W被称为权重(weights),b被称为偏差向量(bias vector),矩阵W和列向量b为该函数的参数(parameters)。
(2)如图三有三个分类器,其中每个图像是一个点,有3个分类器。以红色的汽车分类器为例,红线表示空间中汽车分类分数为0的点的集合,红色的箭头表示分值上升的方向。所有红线右边的点的分数值均为正,且线性升高。红线左边的点分值为负,且线性降低。
(3)偏差和权重的合并技巧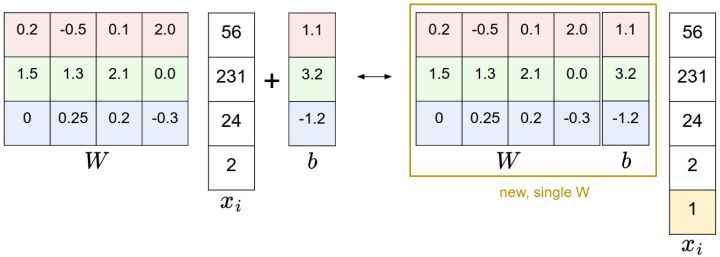
2.2 损失函数 Loss function
神经网络以某个指标(损失函数)为线索寻找最优权重参数。我们将使用损失函数(Loss Function)来衡量我们对结果的不满意程度,直观地讲,当评分函数输出结果与真实结果之间差异越大,损失函数输出越大,反之越小。
2.2.1 均方误差
$$
E=1 \over 2\displaystyle \sum_k{(y_k-t_k)^2}
$$
PS:$y_k$表示神经网络的输出,$t_k$表示监督数据,$k$表示数据的维数。
2.2.2 交叉熵误差
$$
E=-\displaystyle \sum_k{y_klogy_k}
$$
PS:$log$表示($log_e$),$y_k$表示神经网络的输出,$t_k$表示正确解标签。
2.2.3 多类支持向量机损失 Multiclass Support Vector Machine Loss
SVM分类器想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值 Δ ( Δ 值一般取1,代表间隔)。
SVM的损失函数:第i个数据中包含图像$x_i$的像素和代表正确类别的标签$y_i$。针对第j个类别的得分就是第j个元素:$s_j=f(x_i,W)j$,针对第i个数据的多类SVM的损失函数定义如下:
$$
L_i=\displaystyle\sum_{j\neq y_i}{max(1,s_j-s{y_i}+1)}
$$
2.2.4 Softmax分类器
Softmax分类器就可以理解为逻辑回归分类器面对多个分类的一般化归纳。SVM将输出[公式]作为每个分类的评分(因为无定标,所以难以直接解释)。
(1)Softmax函数:
$$
y_k={exp(a_k)} \over {\sum^n_{i=1}exp(a_i)}
$$
PS:假设输出层共有n个神经元,计算第k个神经元的输出$y_k$。分子是输入信号$a_k$的指数函数,分母是所有输入信号的指数函数的和。
Softmax函数的缺陷:溢出问题。($e^1000$的结果返回inf,在超大值之间进行除法运算,结果会出现”不确定”的情况。)
Softmax函数的改进:
$$
y_k={exp(a_k+C^{‘})} \over {\sum^n_{i=1}exp(a_i+C^{‘})}
$$
PS:$C^{‘}$可以为任意值,但为了防止溢出,一般使用输入信号中的最大值。
(2)Softmax的损失函数:
$$
L=-log({e^s{y_i}\over {\sum_j{e^{s_j}}}})
$$
(3)Softmax函数的特征:
①输出是0.0到1.0之间(概率),输出总和为1;
②神经网络只把输出最大的神经元所对应的类别作为识别结果,并且位置不变。
(4)SVM和Softmax的比较
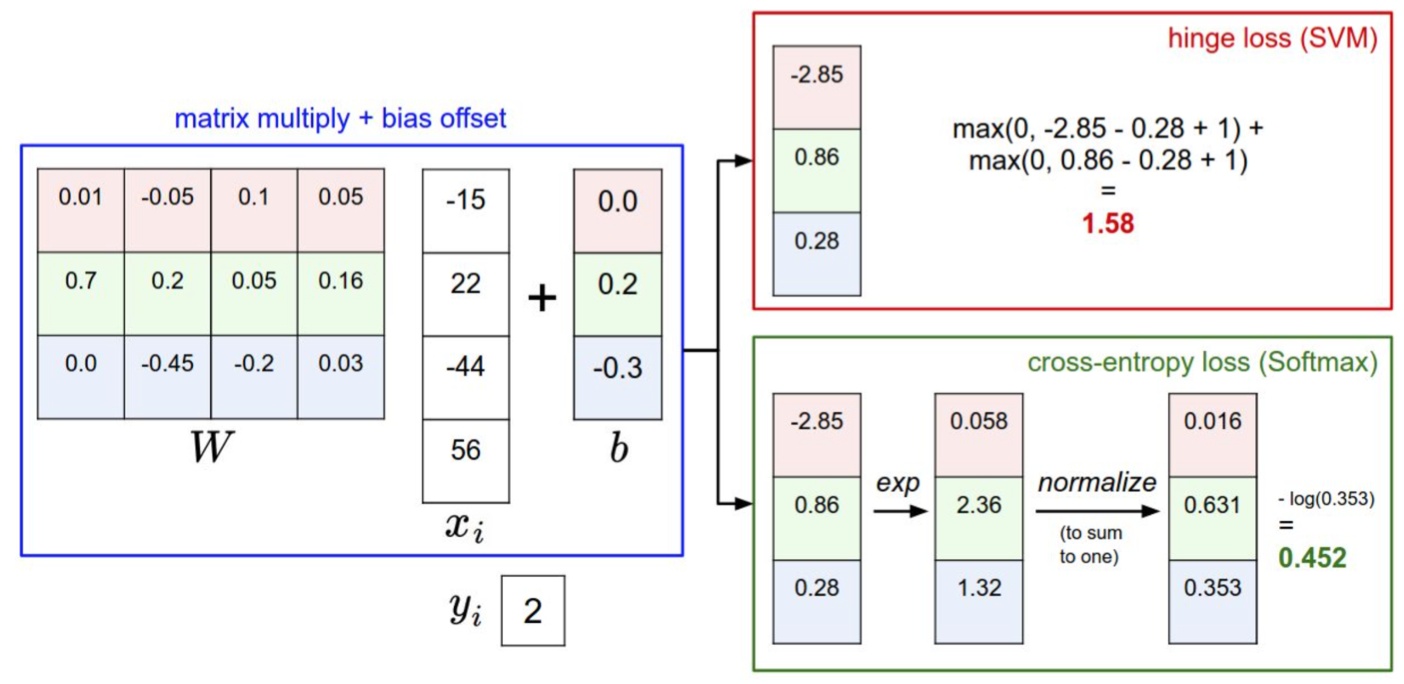
2.3 最优化Optimization
2.3.1 参数更新
神经网络的学习目的是找到使损失函数的值尽可能小的参数,这是寻找最优参数的问题,解决这个问题的过程称为==最优化==。
策略#1:随机搜索
随机尝试很多不同的权重,然后看其中哪个最好。
核心思路:迭代优化。
我们的策略是从随机权重开始,然后迭代取优,从而获得更低的损失值。
策略#2:随机本地搜索
第一个策略可以看做是每走一步都尝试几个随机方向,如果某个方向是向山下的,就向该方向走一步。这次我们从一个随机$W$开始,然后生成一个随机的扰动$\partial W$,只有当$W+\partial W$的损失值变低,我们才会更新。
策略#3:随机梯度下降法(SGD)
使用参数的梯度,沿梯度方向更新参数,并重复这个步骤多次,从而逐渐靠近参数。
SGD策略:朝着当前所在位置的坡度最大的方向前进。
公式:$W{\leftarrow}W-\eta{\frac{\partial L}{\partial W}}$
SGD的缺点:如果函数的形状非均向,搜素的路径就会非常低效。SGD低效的根本原因是,梯度的方向并没有指向最小值的方向。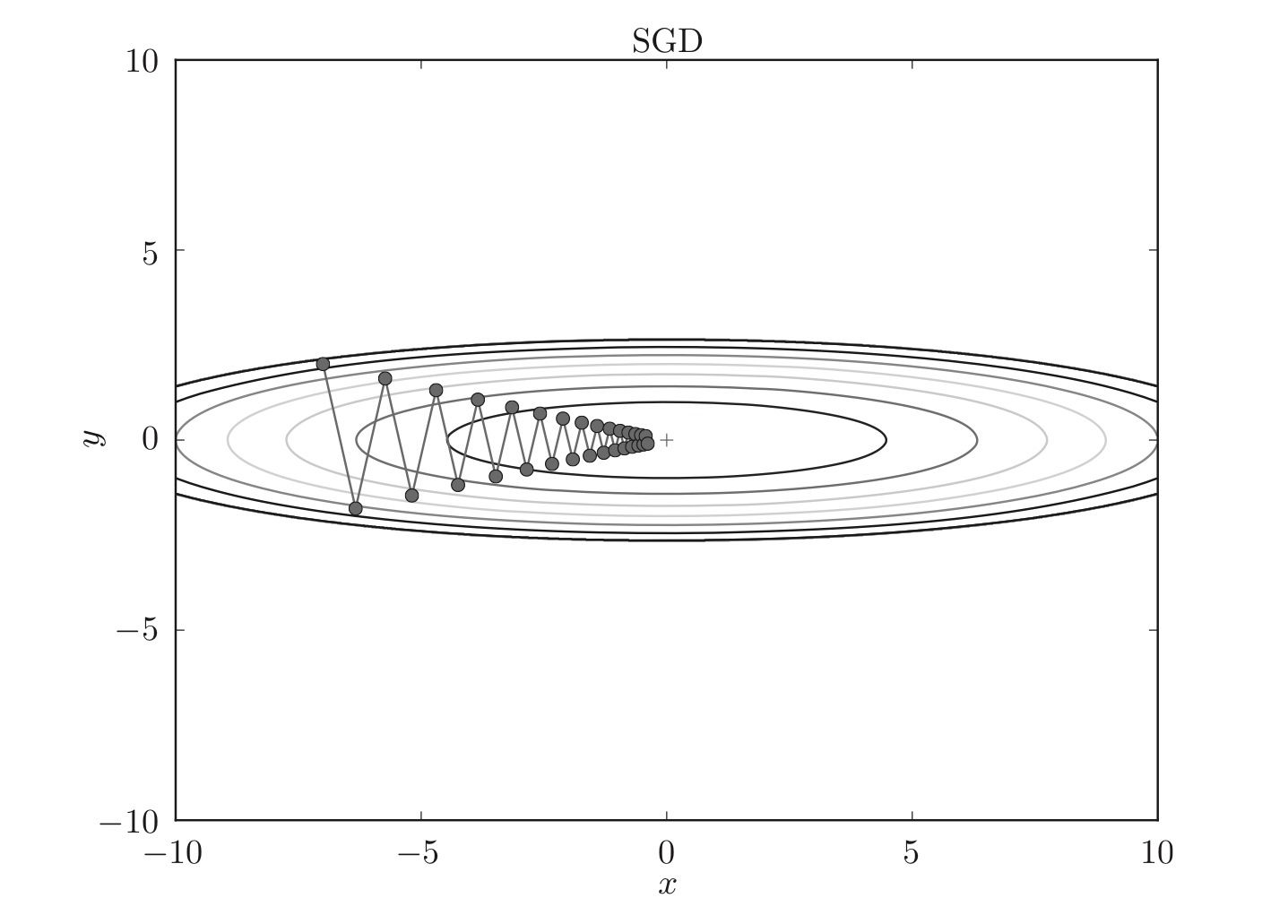
策略#4:Momentum
公式:
$$
v{\leftarrow}\alpha v-\eta{\frac{\partial L}{\partial W}}
$$
$$
W{\leftarrow}W+v
$$
Momentum更新路径就像小球在碗中滚动一样。和SGD相比,可以更快地朝$x$轴方向靠近,减弱“之”字形的变动程度。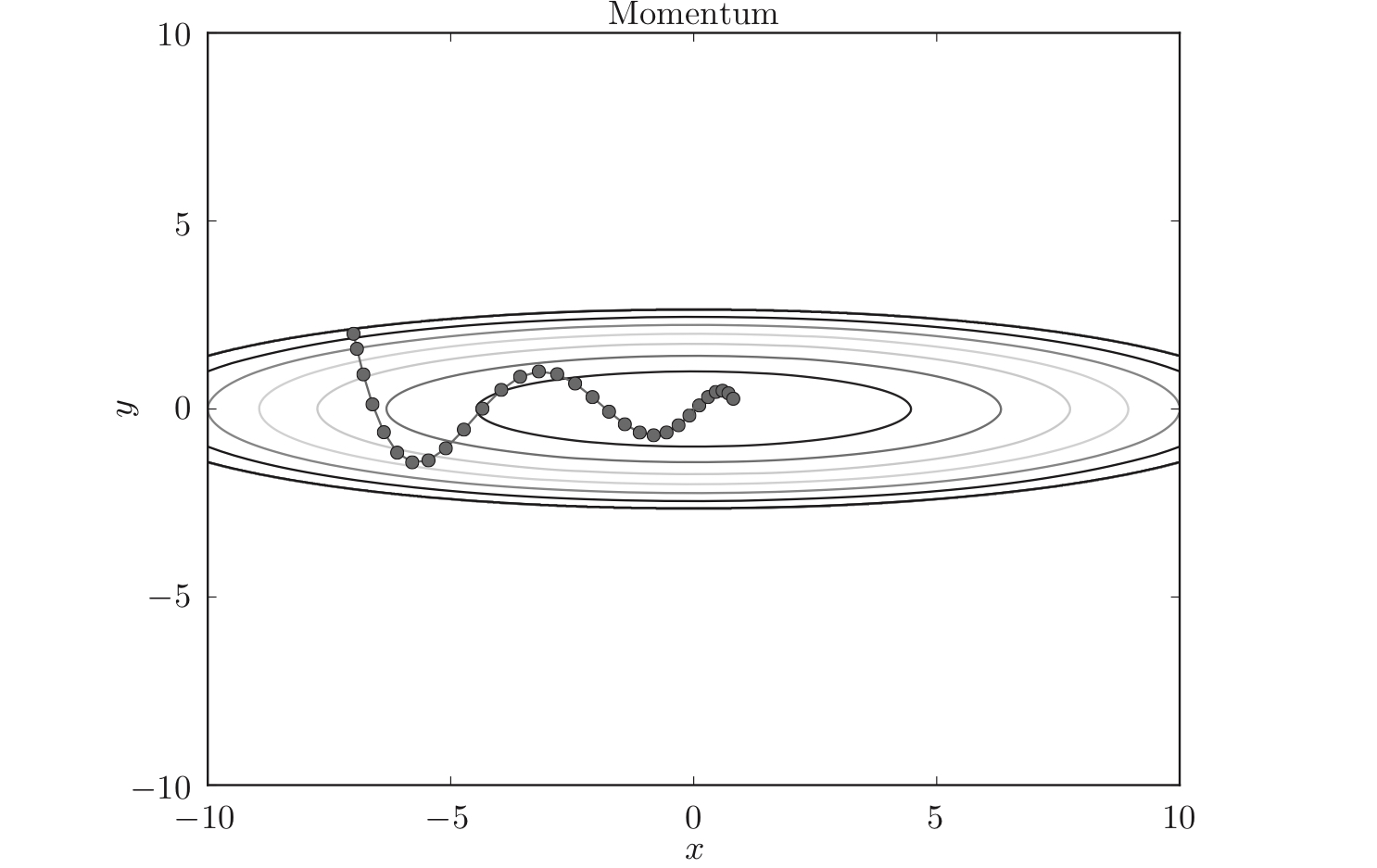
策略#5:AdaGrad
学习率衰减:随着学习的进行,是学习率追渐减小。
AdaGrad:为参数的每个元素适当调整学习率,与此同时进行学习。
公式:
$$
h{\leftarrow}h+{\frac{\partial L}{\partial W}} \cdot {\frac{\partial L}{\partial W}}
$$
$$
W{\leftarrow}W-\eta{1 \over \sqrt h}{\frac{\partial L}{\partial W}}
$$
如图,函数的取值高效地向着最小值移动。由于$y$轴方向上的梯度较大,因此刚开始变动较大,但是后面会根据这个较大的变动按比例进行调整,减小更新的步伐。因此,$y$轴方向上的更新程度被减弱,“之”字形的变动程度有所衰减。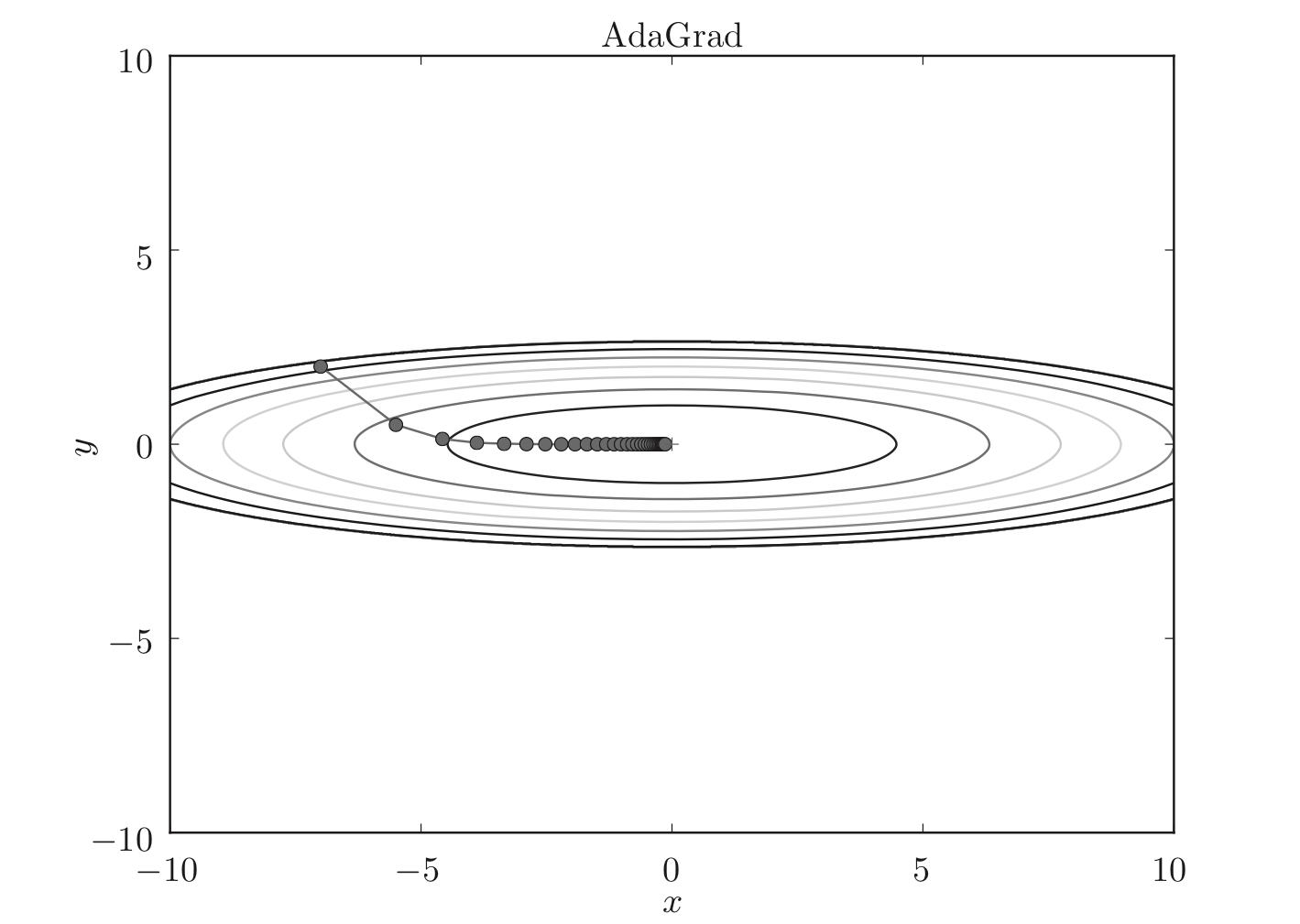
策略#6:Adam
Momentum参照小球在碗中滚动的物理规则进行移动,AdaGrad为参数的每个元素适当地调整更新步伐。两者融合就是Adam方法的基本思路。
Adam的特征:进行超参数的“”。
如图,相比Momentum,Adam的小球左右摇晃的程度有所减轻。
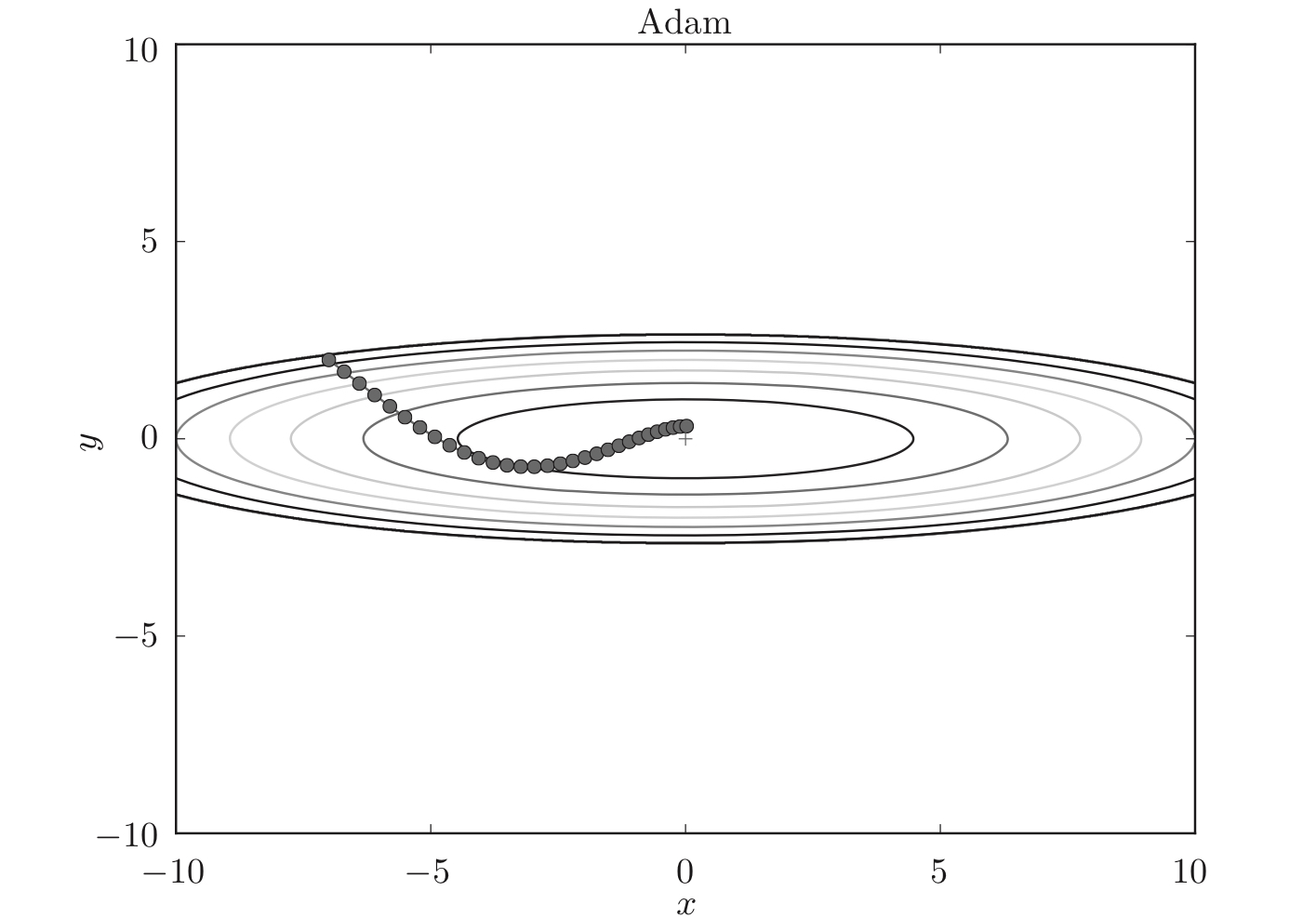
三、神经网络与反向传播
3.1 神经网络 Neural Network
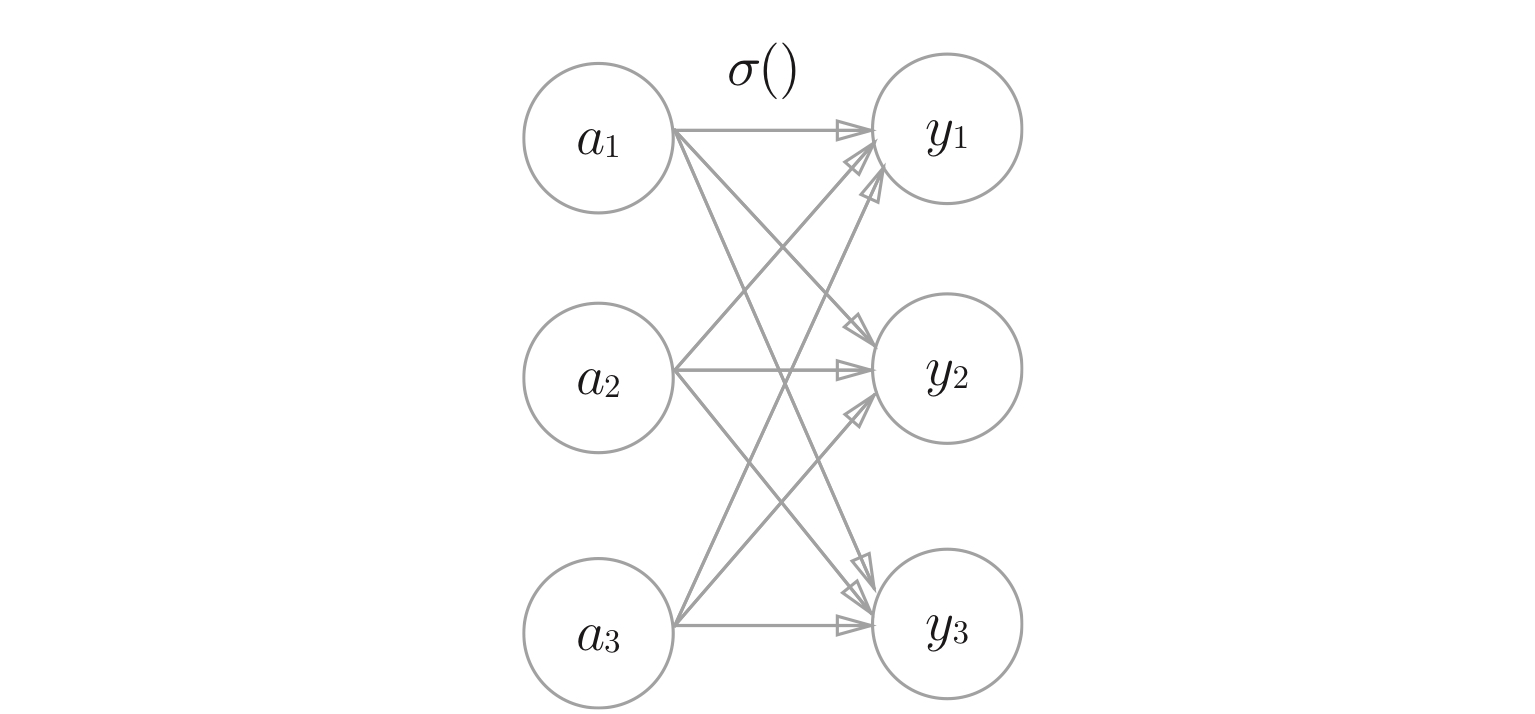
如图,神经网络的例子: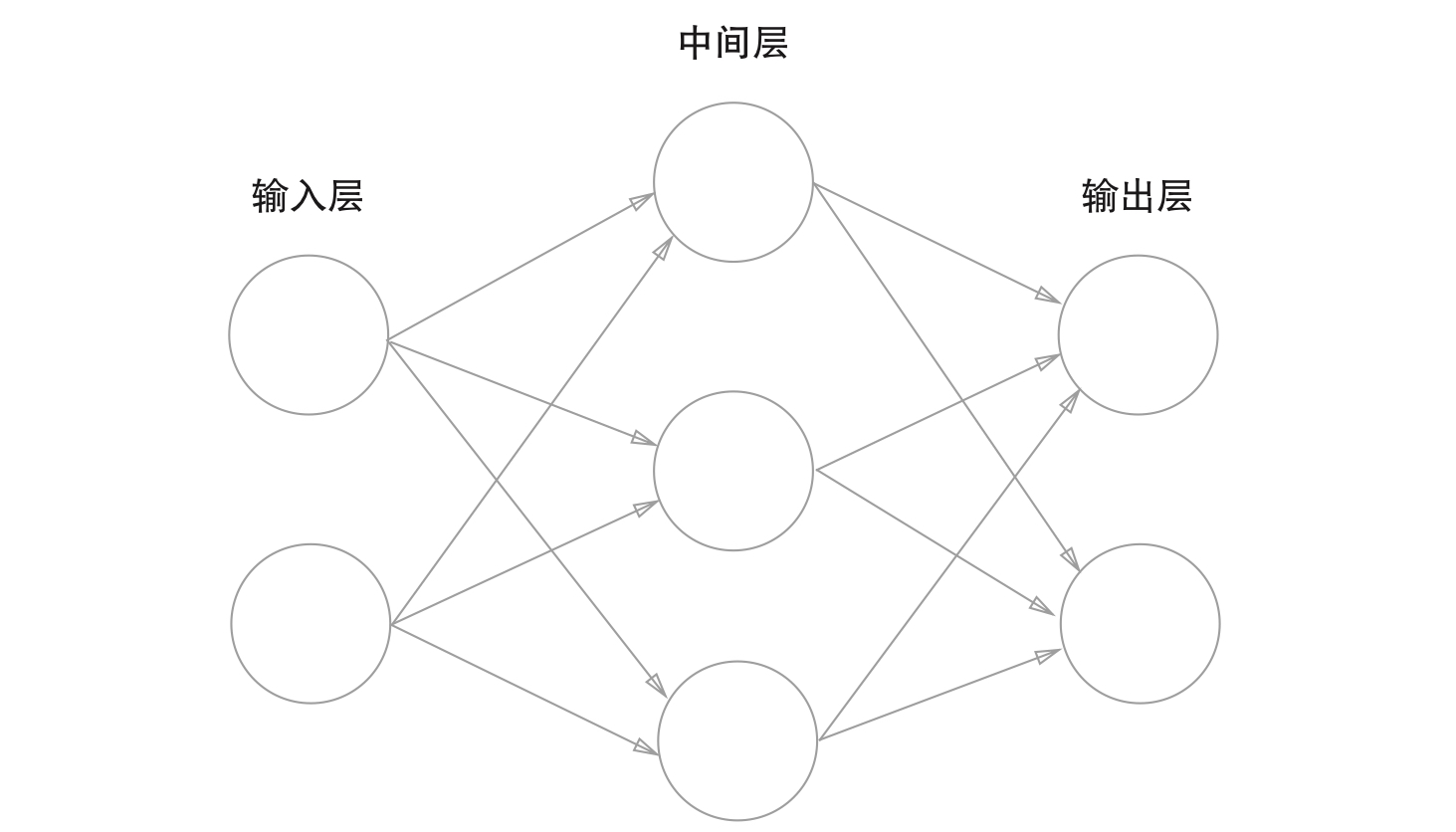
如图,显示激活函数的计算过程: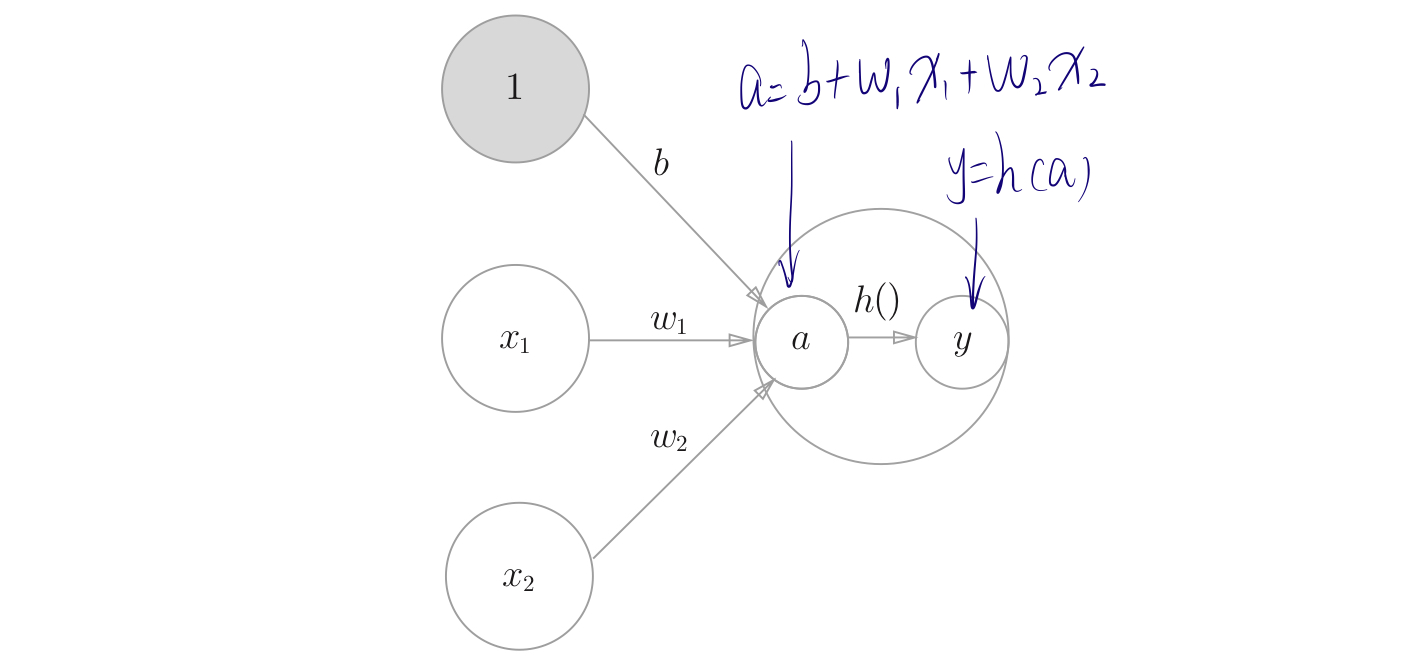
3.1.1 激活函数 Activation Function
激活函数以阈值为界,一旦输入超过阈值,就切换输出。
3.1.1.1 sigmoid函数
公式:
$$
h(x)={1 \over {1+exp(-x)}}
$$
如图,sigmoid函数具有平滑性,可以返回0.0~1.0的实数(神经网络中流动的是连续的实数值信号)。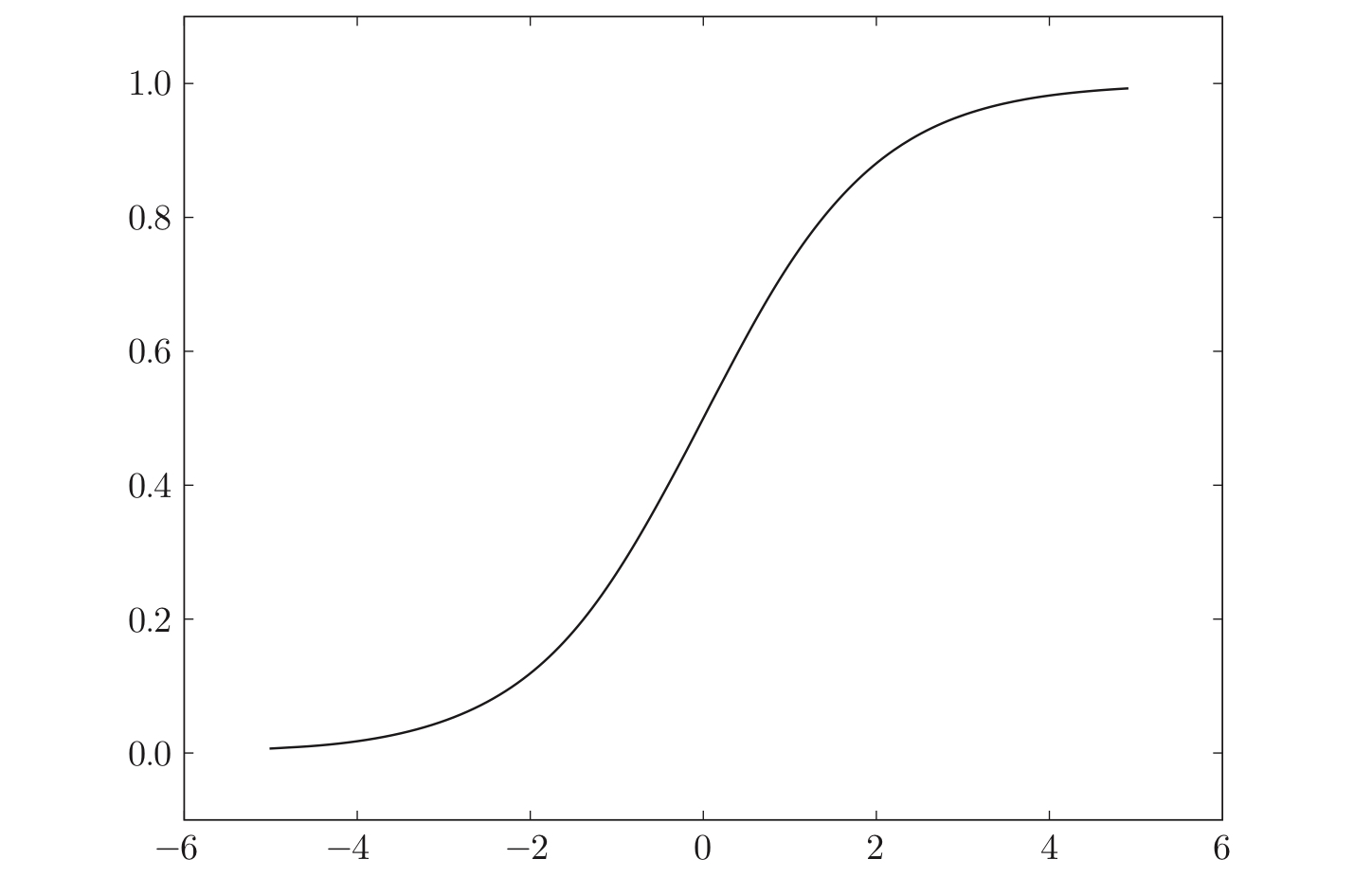
3.1.1.2 ReLU函数
$$
f(x) = \begin{cases}
0 & x < 0 \
x & x \geq 1
\end{cases}
$$
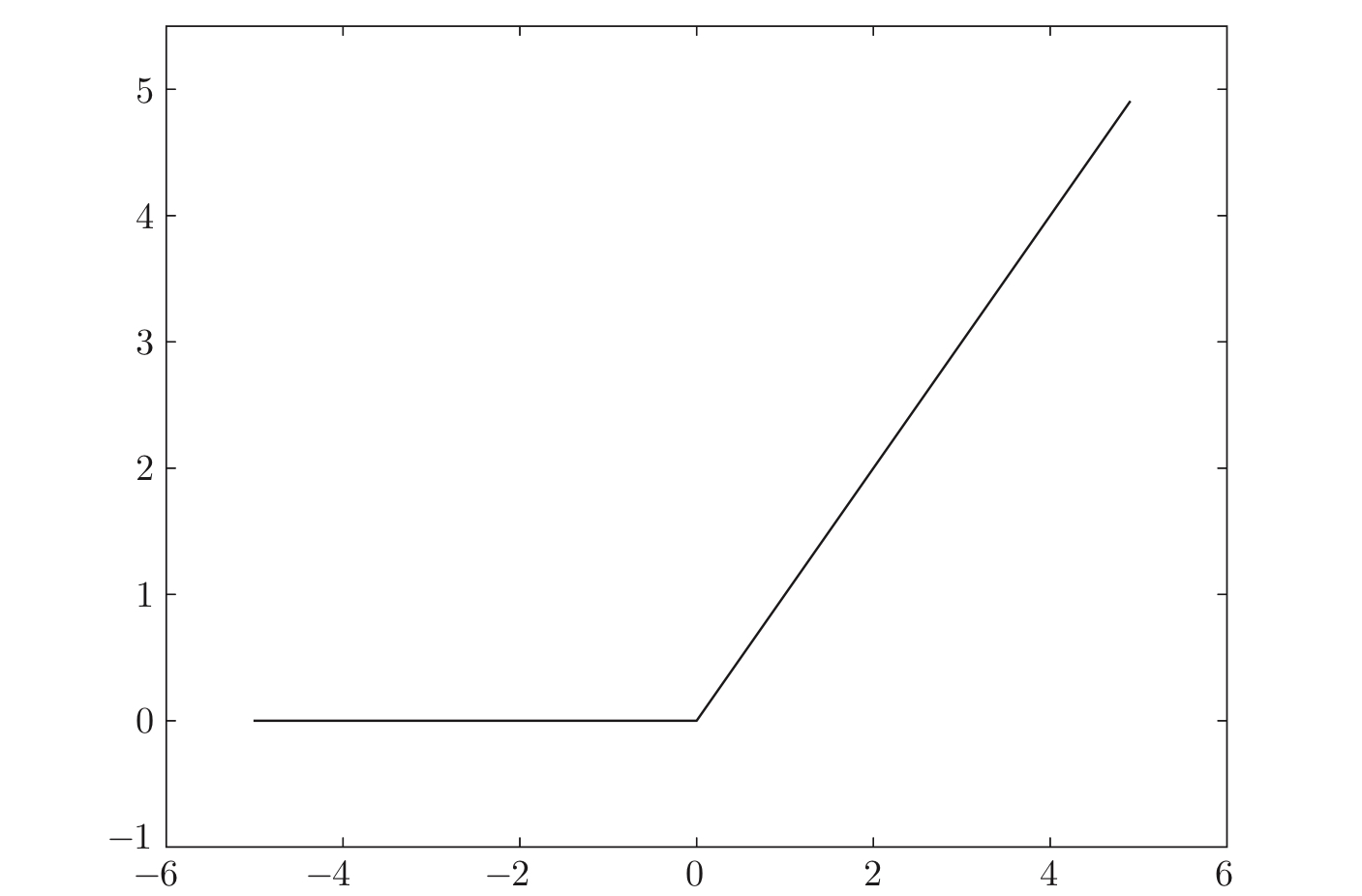
3.1.1.3 汇总
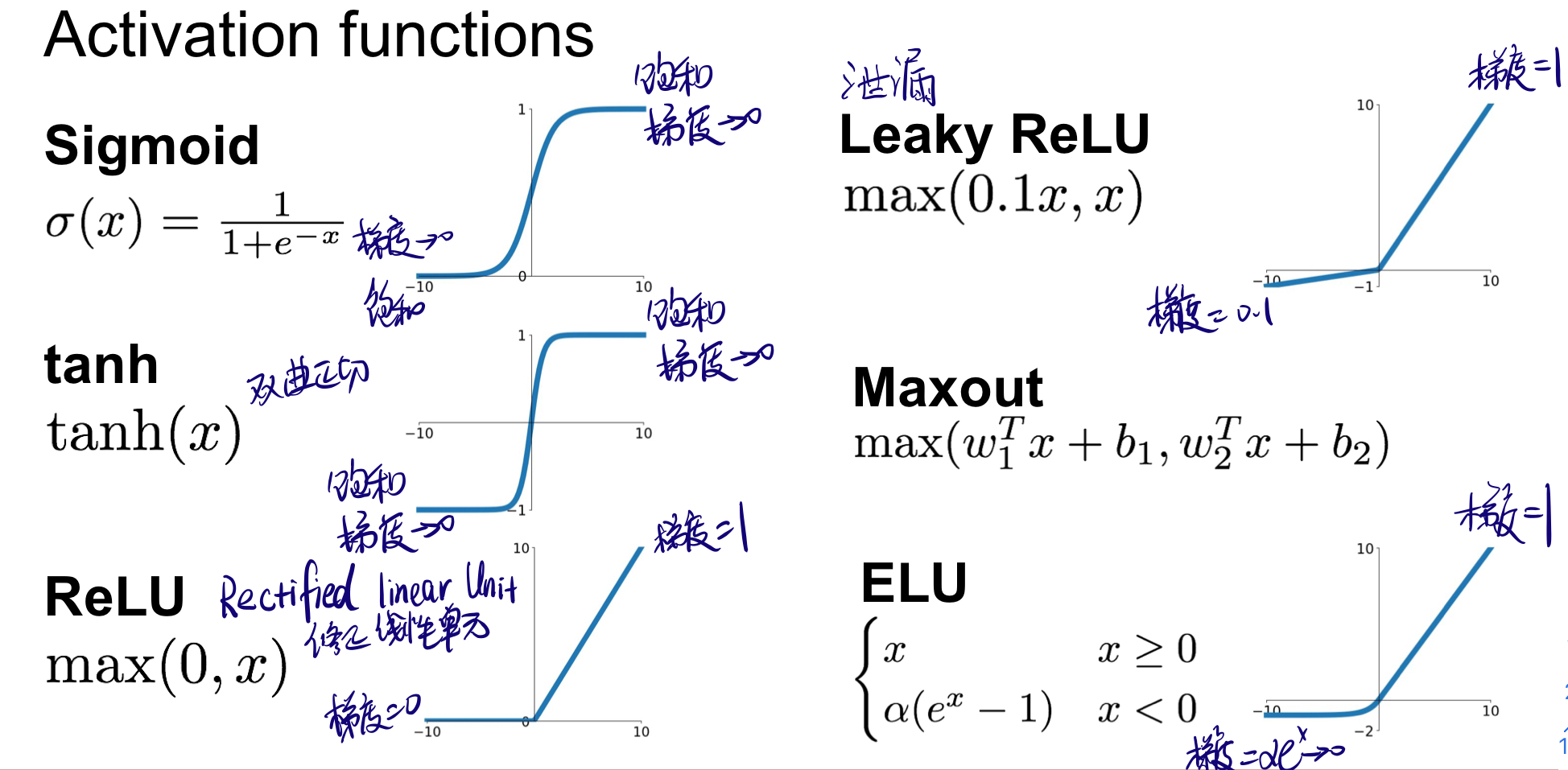
3.1.2 前向传播
从输入层到第一层中激活函数的计算过程,隐藏层的加权和(加权信号和偏置的总和)用$a$表示,被激活函数转换后的信号用$z$表示,$h()$表示激活函数(sigmoid函数)。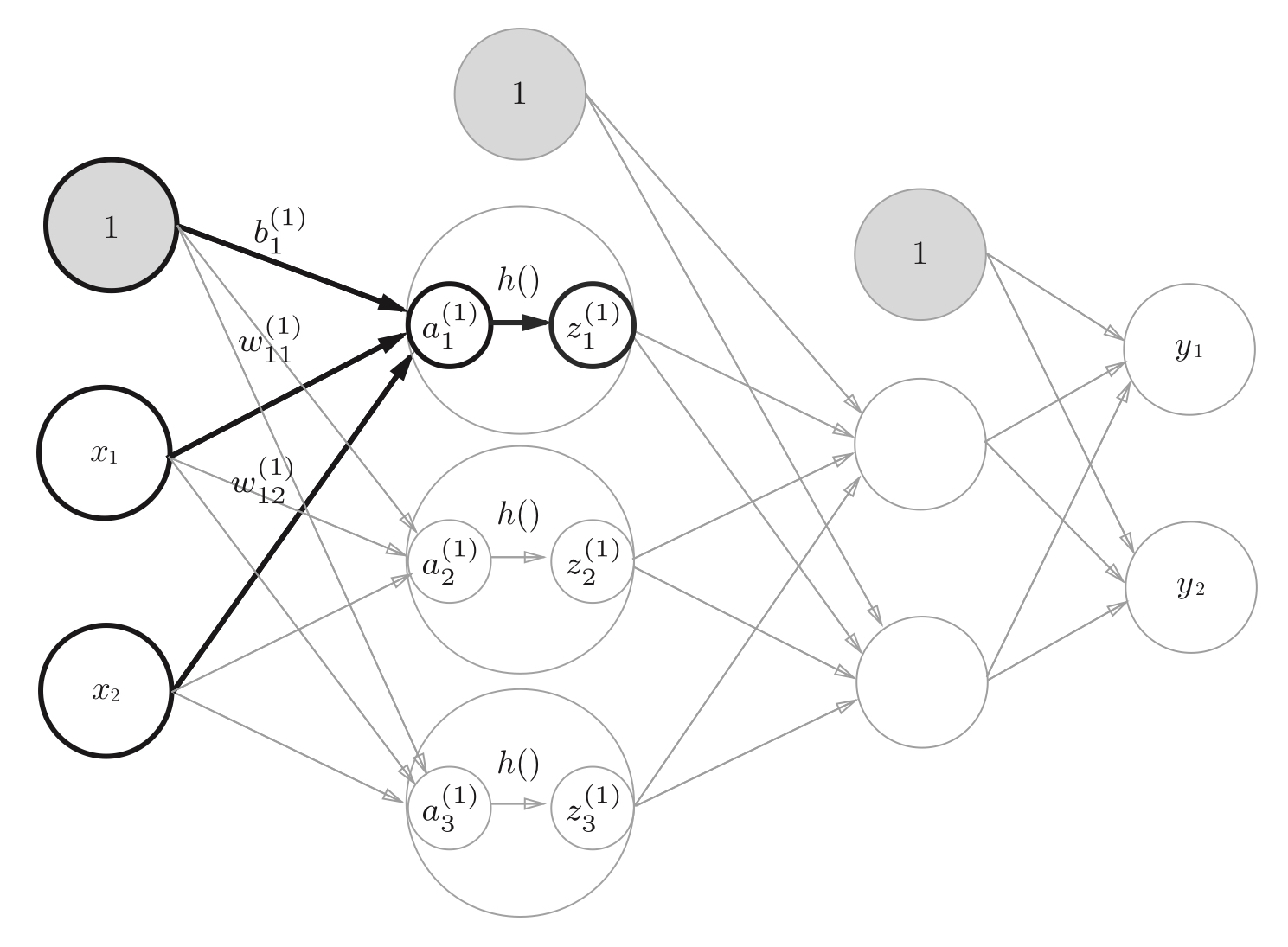
从第一层到第二层的信号传递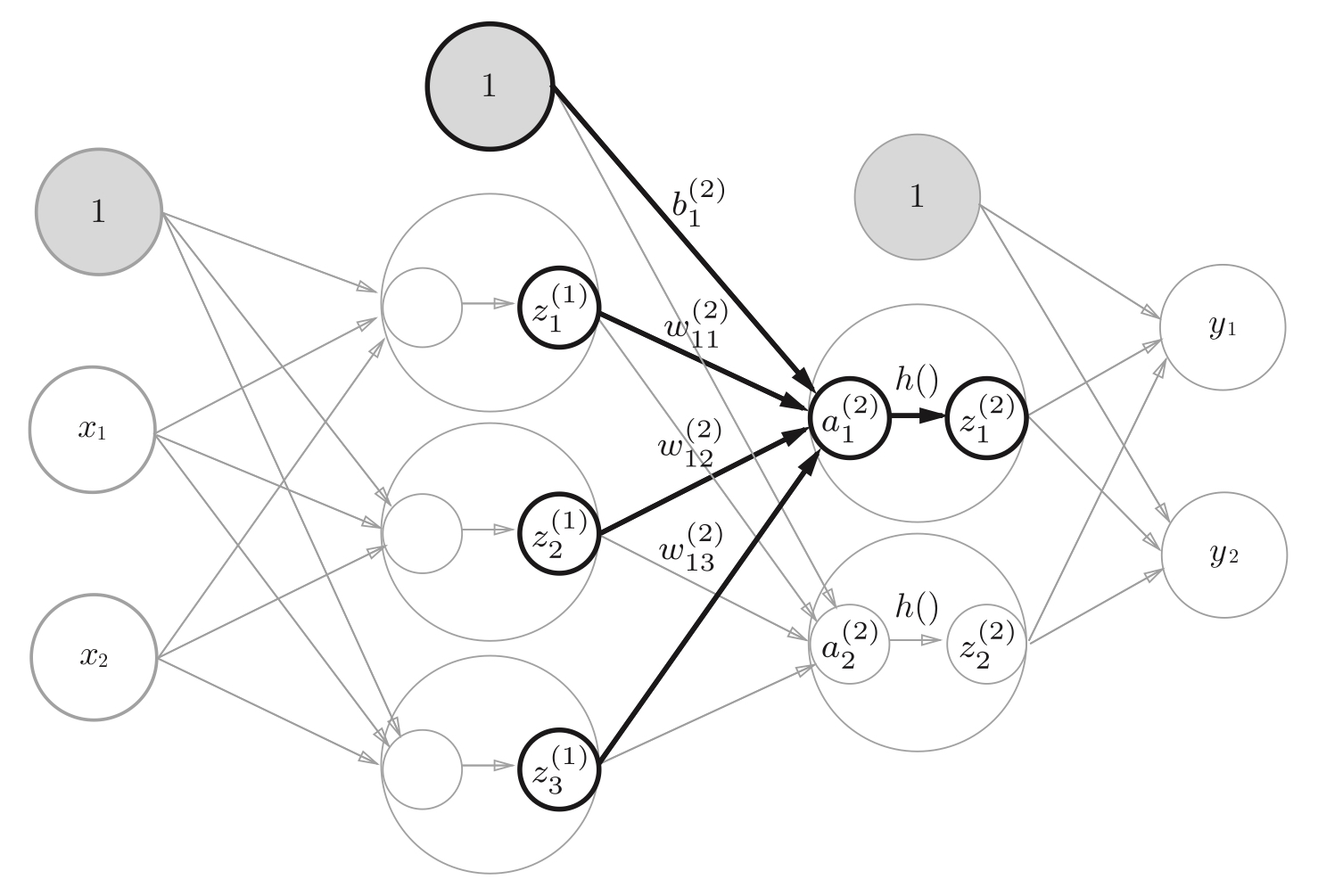
从第二层到输出层的信号传递,输出层的激活函数与隐藏层的不同。一般地,1⃣️回归问题可以使用恒等函数;2⃣️二元分类问题可以使用sigmoid函数;3⃣️多元分类问题可以使用sofetmax函数。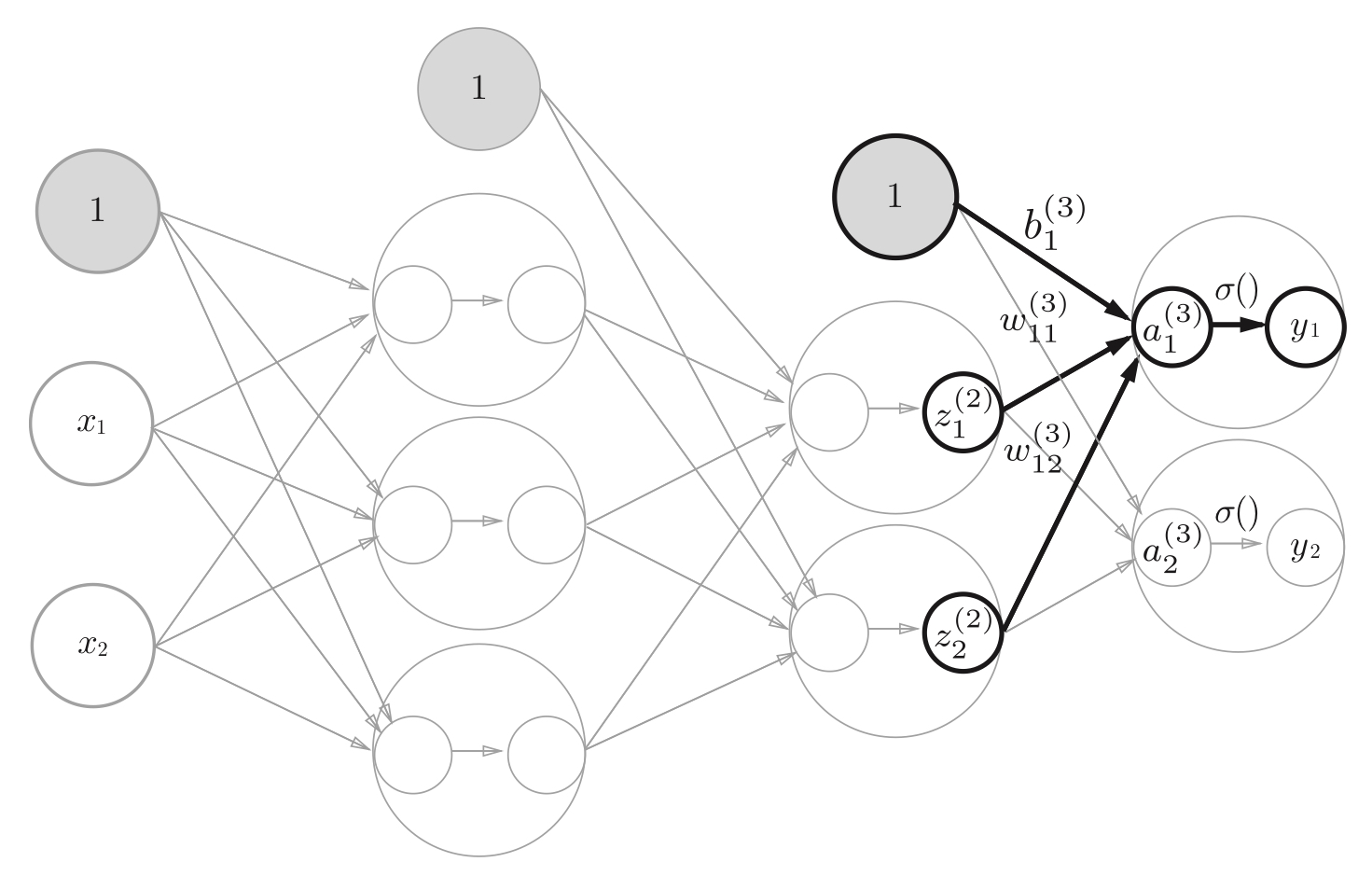
3.1.3 误差反向传播
全连接层的反向传播。
加法节点的反向传播将输入信号输出到下一个节点;乘法的反向传播会讲上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。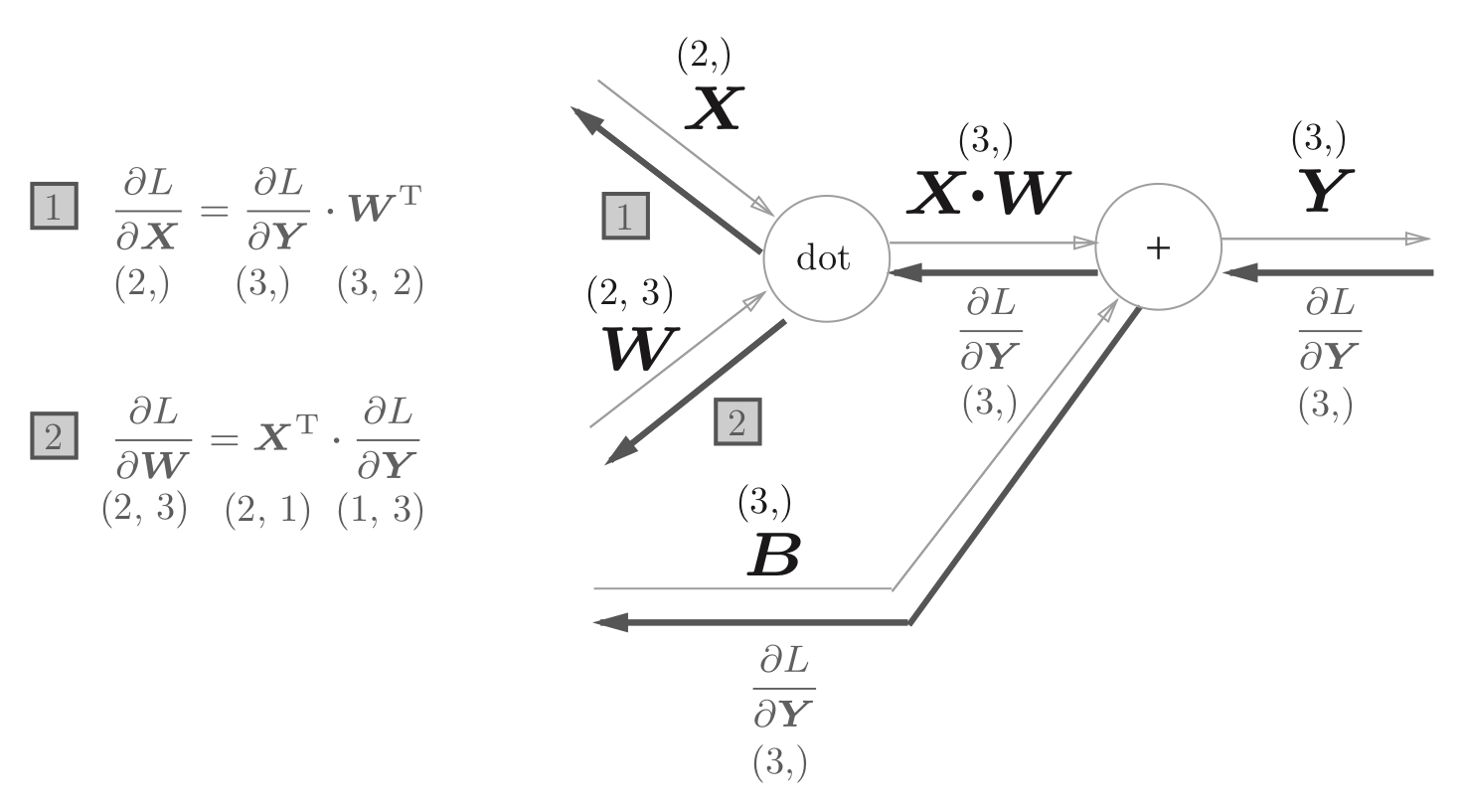
输出层Softmax层的反向传播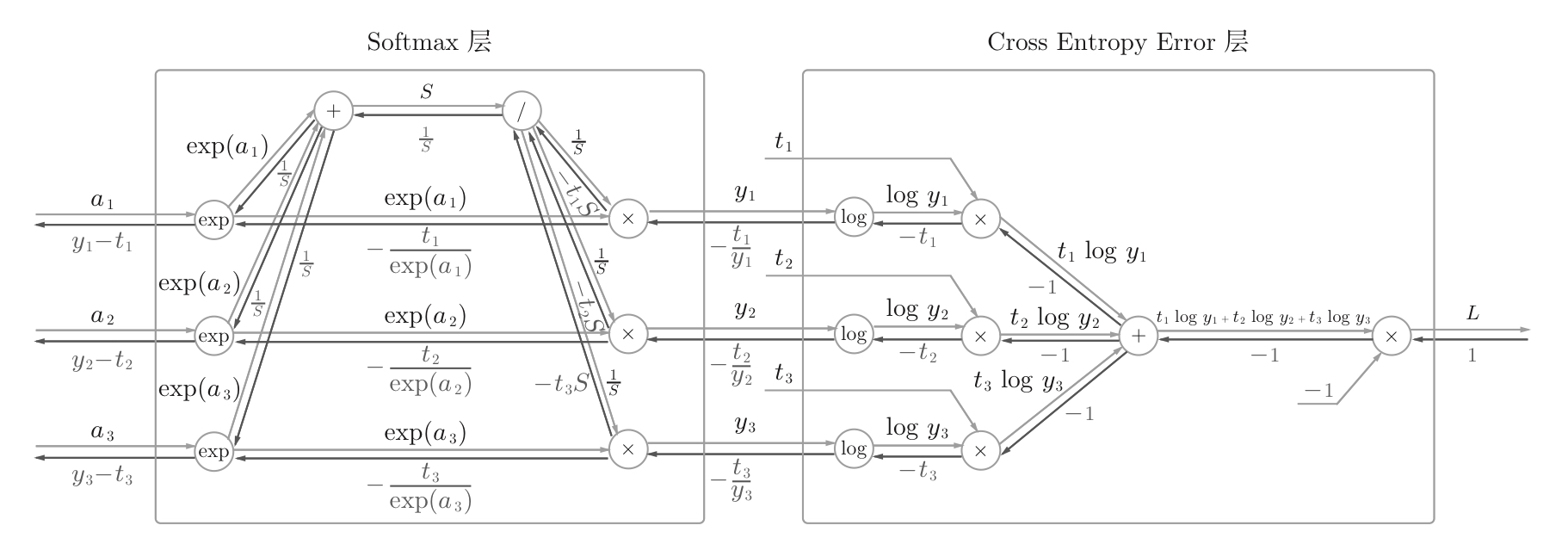
3.1.4 神经网络实现全貌

四、卷积神经网络
4.1 CNN整体结构

4.2 卷积层
全连接层存在数据的形状被“忽视”的问题,而卷积层可以保持形状不变。
4.2.1 卷积计算过程
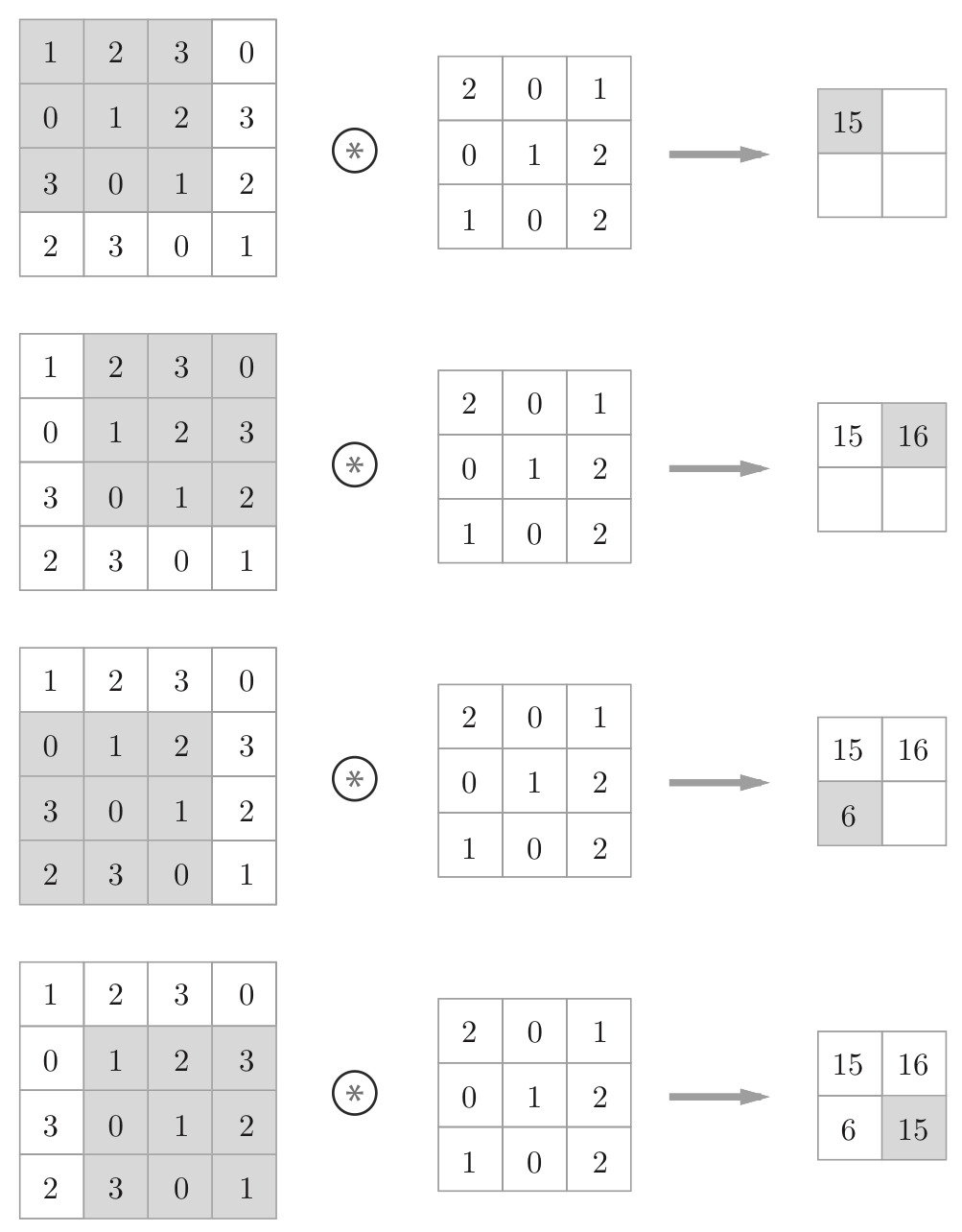
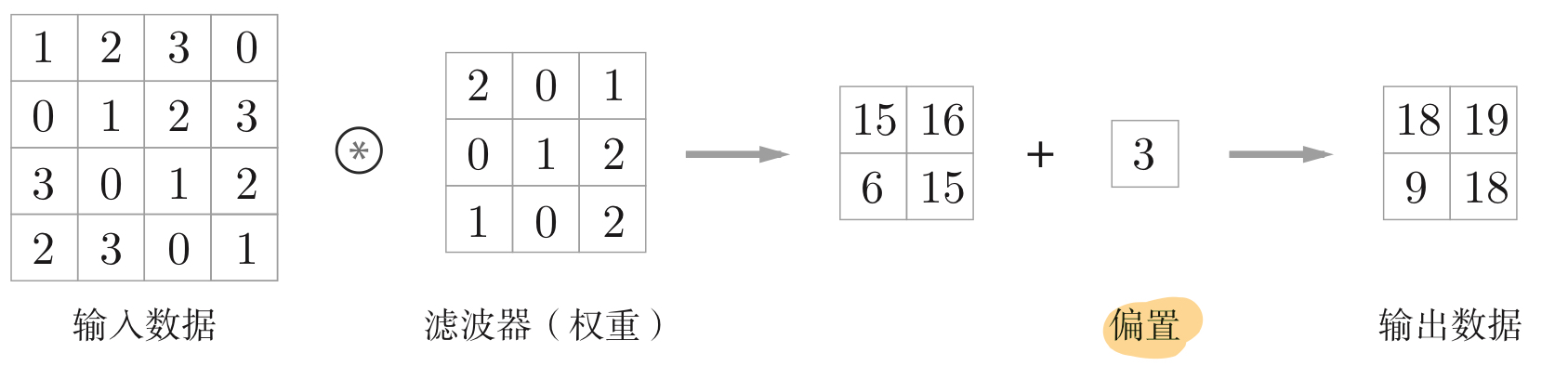
4.2.2 填充
使用填充主要是为了调整输出的大小。因为如果每次进行卷积运算都会缩小空间,那么在某个时刻输出大小就有可能变为1,导致无法再应用卷积运算。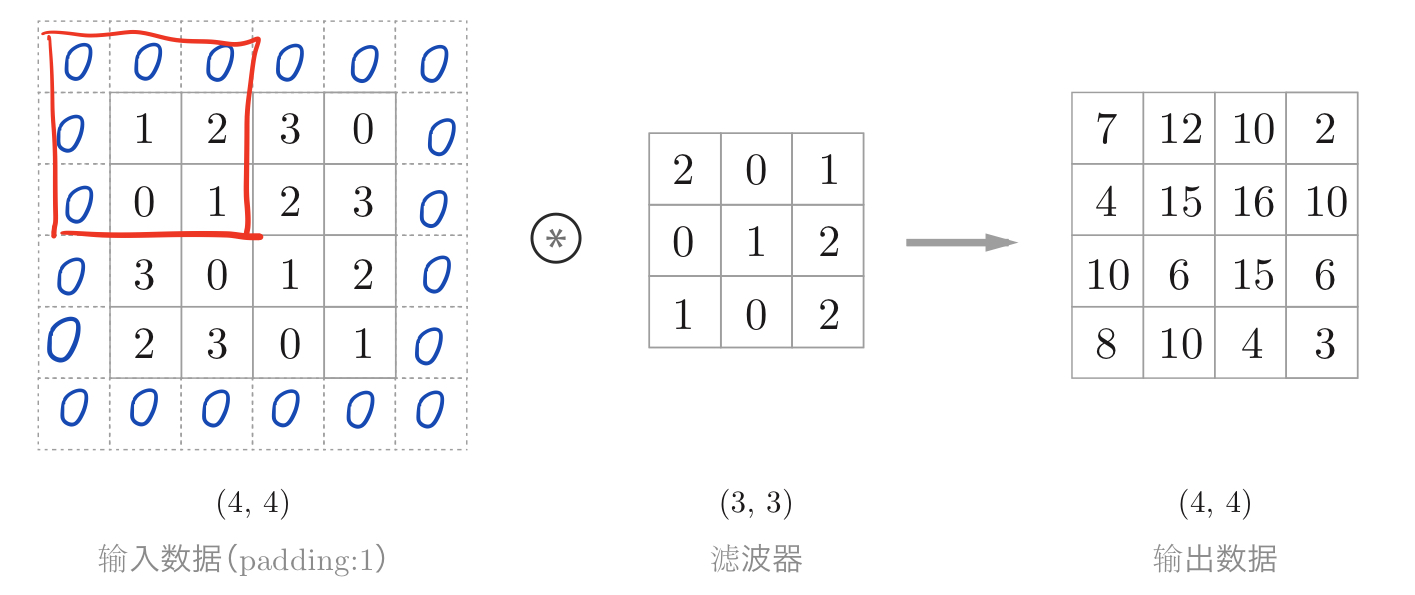
4.2.4 三维卷积
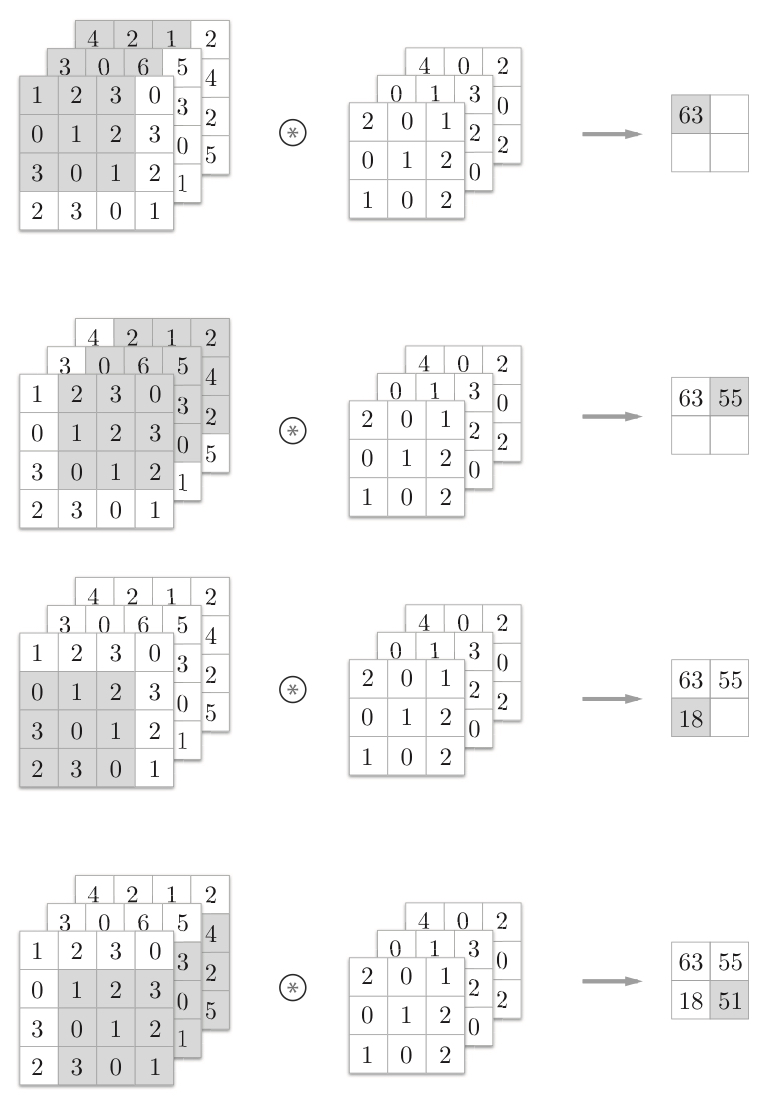
PS:通道数只能设定为和输入数据的通道数相同的值。
4.3 池化层
池化是缩小高、长方向上的空间的运算。下图为Max池化的处理顺序。一般来说,池化的窗口大小会和步幅设定成相同的值。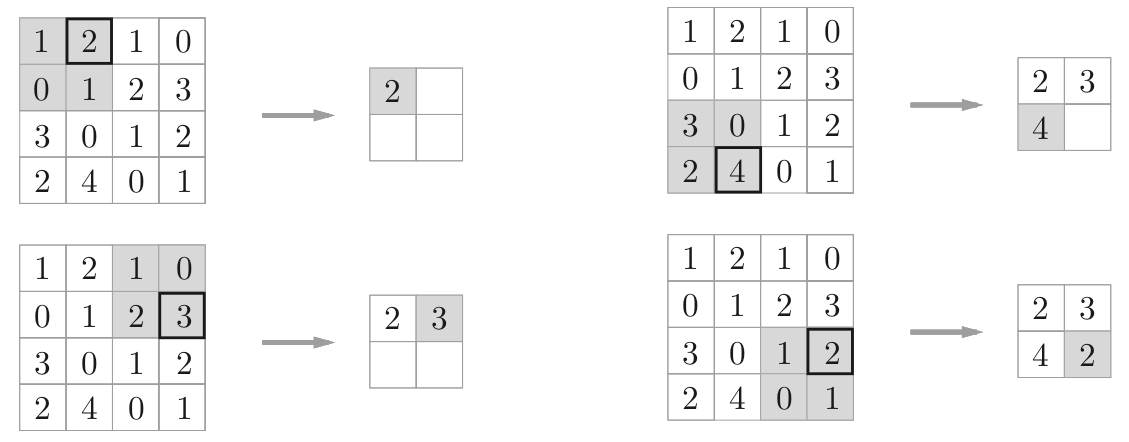
池化层的特征:1⃣️没有要学习的参数;2⃣️通道数不发生变化;3⃣️对微小的位置变化具有鲁棒性(健壮)
PS:鲁棒性——在异常和危险情况下系统生存的能力。
4.4 CNN的可视化
如果堆叠了多层卷积层,则随着层次加深,提取的信息也愈加复杂、抽象;随着层次加深,神经元从简单的形状向“高级”信息变化。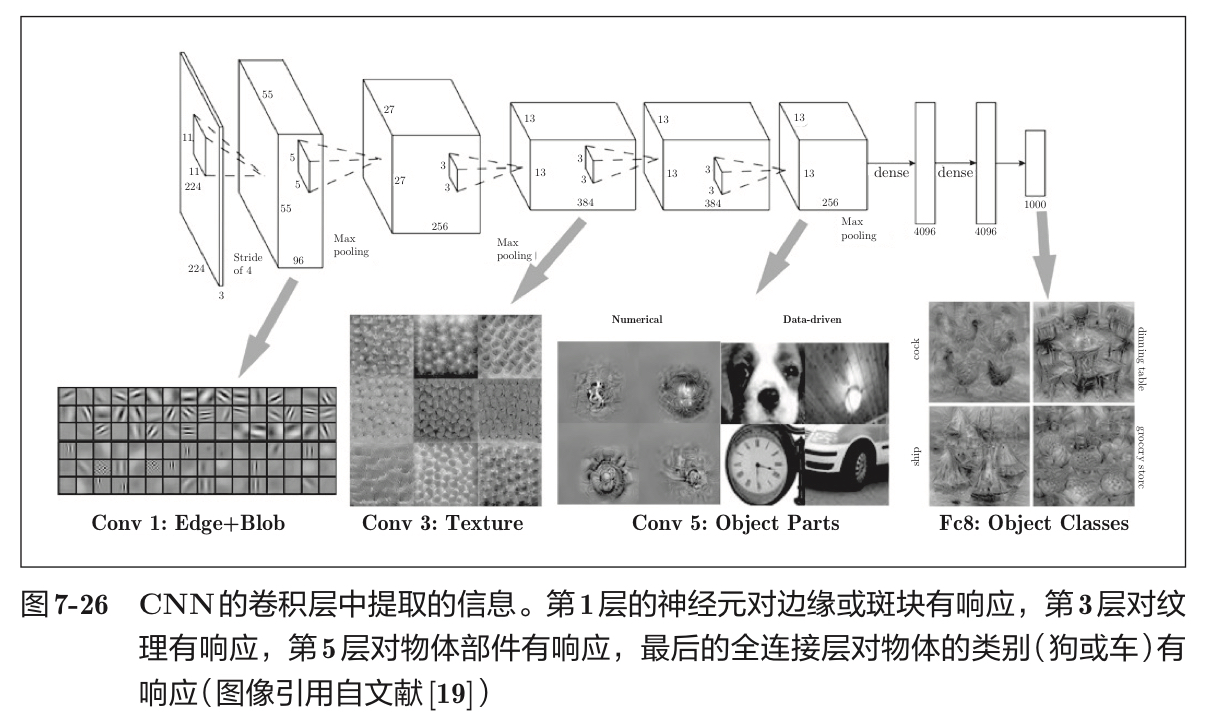
五、循环神经网络
牛逼的网站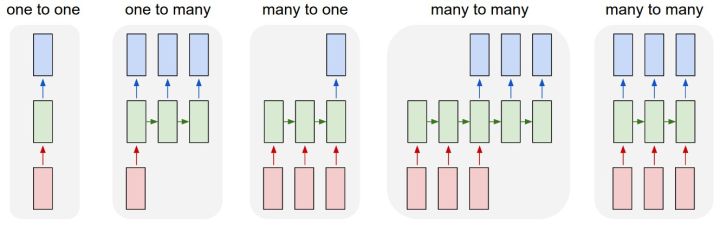
循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x,还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重。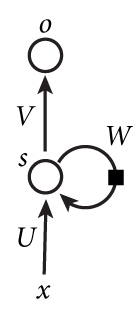
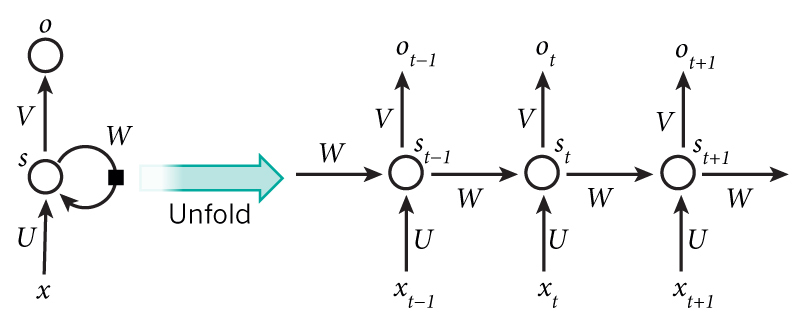
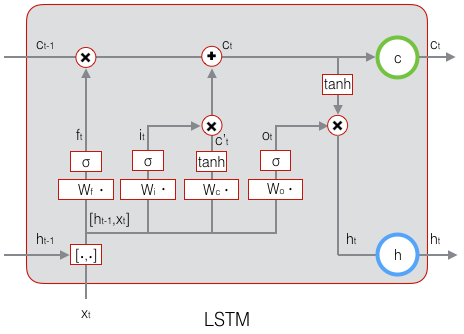
LSTM