《解析深度学习》阅读笔记

解析深度学习

    记录一些刚开始没理解的名词。

一  深度相比宽度，在网络复杂性中提升更有效

1.1  网络深度

    深度，即网络的层数，加深网络深度可以提升性能。

1.1.1  更好地拟合特征

    现在的深度学习网络结构的主要模块是卷积、池化、激活，这是一个标准的非线性变换模块。更深的模型，意味着更好的非线性表达能力，可以学习更加复杂的变换，从而可以拟合更加复杂的特征输入。

1.1.2   不同深度的网络层学习到不同特征

1.2  网络宽度

    宽度，即通道(channel)的数量，是让每一层学习到更加丰富的特征，比如不同方向，不同频率的纹理特征。
    下面是AlexNet模型的第一个卷积层的96个通道，尽管其中有一些形状和纹理相似的卷积核(这将成为优化宽度的关键)，还是可以看到各种各种的模式。

    有的是彩色有的是灰色，说明有的侧重于提取纹理信息，有的侧重于提取颜色信息。

    参考：https://www.zhihu.com/question/291790340

1.3  网络宽度和深度谁更加重要？

    两者都很重要，但目前的研究是模型性能对深度更加敏感，而调整宽度更加有利于提升模型性能。

•  深度相关计算量是O(N)，宽度则是O(N * N)，宽度更加敏感；
•  弥补深度不足需要的代价更高，而增加宽度提升性能更快；
•  增加宽度对GPU更加友好。
      一般，优先调整网络的宽度。

二  低秩近似、奇异值分解

2  奇异值分解

2.1  五个定理

• 定理一：A是对称矩阵，则不同特征值对应的特征向量是正交的。
• 定理二：矩阵和它的转置具有相同的特征值。
• 定理三：半正定矩阵的特征值均大于等于零。
• 定理四：若满足,则称是单位正交矩阵。
• 定理五：若矩阵的秩为r，则和秩均为r。

2.2  奇异值分解（SVD）

[定义一]给定一个大小为 [公式] 的实对称矩阵 [公式] ，若对于任意长度为 [公式] 的非零向量 [公式] ，有 [公式] 恒成立，则矩阵 [公式] 是一个正定矩阵。

---

[定义二]给定一个大小为 [公式] 的实对称矩阵 [公式] ，若对于任意长度为 [公式] 的向量 [公式] ，有 [公式] 恒成立，则矩阵 [公式] 是一个半正定矩阵。

    设矩阵$X \in R^{mxn}$，秩为$r$，$r \leq min(m,n)$，则该矩阵可以分解为：

$X=\left[ \begin{matrix} u_1 & u_2 \cdots u_r\end{matrix} \right]\left[ \begin{matrix} \lambda_1 & & \\ &\lambda_2 & \\ & &\ddots\\ & & & \lambda_r\\\end{matrix}\right]\left[ \begin{matrix} v^T_1 \\ v^T_2 \\\vdots \\ v^T_r\end{matrix} \right] $     也可表示为： $X=\sum_{r=1}^n{\lambda_iu_iv^T_i}$     其中：$\lambda_i$为矩阵$XX^T$（或者$X^TX$）的非零向量,$u_i$为$XX^T$的对应特征向量，$v_i$为$X^TX$的对应特征向量，$\lambda_1 \ge \lambda_2 \ge···\lambda_r$。

2.3  低秩近似

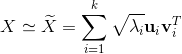
    对于现实中比较好的图片，往往秩比较低的，也就是图像比较规整，重点的突出点是有的，但是大部分像素是相似的；假如图片的秩很高，那结果就是图像杂乱无章，或者是噪声比较高。
    因此，在做图像处理时，可以通过降低秩来去除图片中的噪点。

三  数据驱动

    数据驱动是通过移动互联网或者其他的相关软件为手段采集海量的数据，将数据进行组织形成信息，之后对相关的信息进行整合和提炼，在数据的基础上经过训练和拟合形成自动化的决策模型。

四  激活函数

    参数化ReLu作为激活函数的网络要优于使用原始ReLU的网络，同时自由度较大的各通道独享参数的参数化ReLU性能更优。
    ReLU -> Leaky ReLU、参数化ReLu、随机化ReLU和ELU

五  独热编码（one-hot）

    One-Hot编码是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值。然后，每个整数值被表示为二进制向量，除了整数的索引之外，它都是零值，它被标记为1。

    使用one-hot编码，将离散特征的取值扩展到欧氏空间，离散特征的某个取值就对应欧式空间的某个点，让特征之间的距离计算更加合理。

    不需要使用one-hot编码的情况：特征是离散的，并且不用one-hot编码就可以很合理地计算出距离，就没必要进行one-hot编码。
    参考：帅帅的飞猪

六  泛化性

    根据有限样本得到的网络模型对其他变量域也有良好的预测能力。

七  过拟合

    过拟合是指只能拟合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。
    原因：①模型拥有大量参数、表现力强；②训练数集少。

  抑制过拟合：
  ①增加数据量；②适当减小参数数量：正则化（权值衰减）、dropout。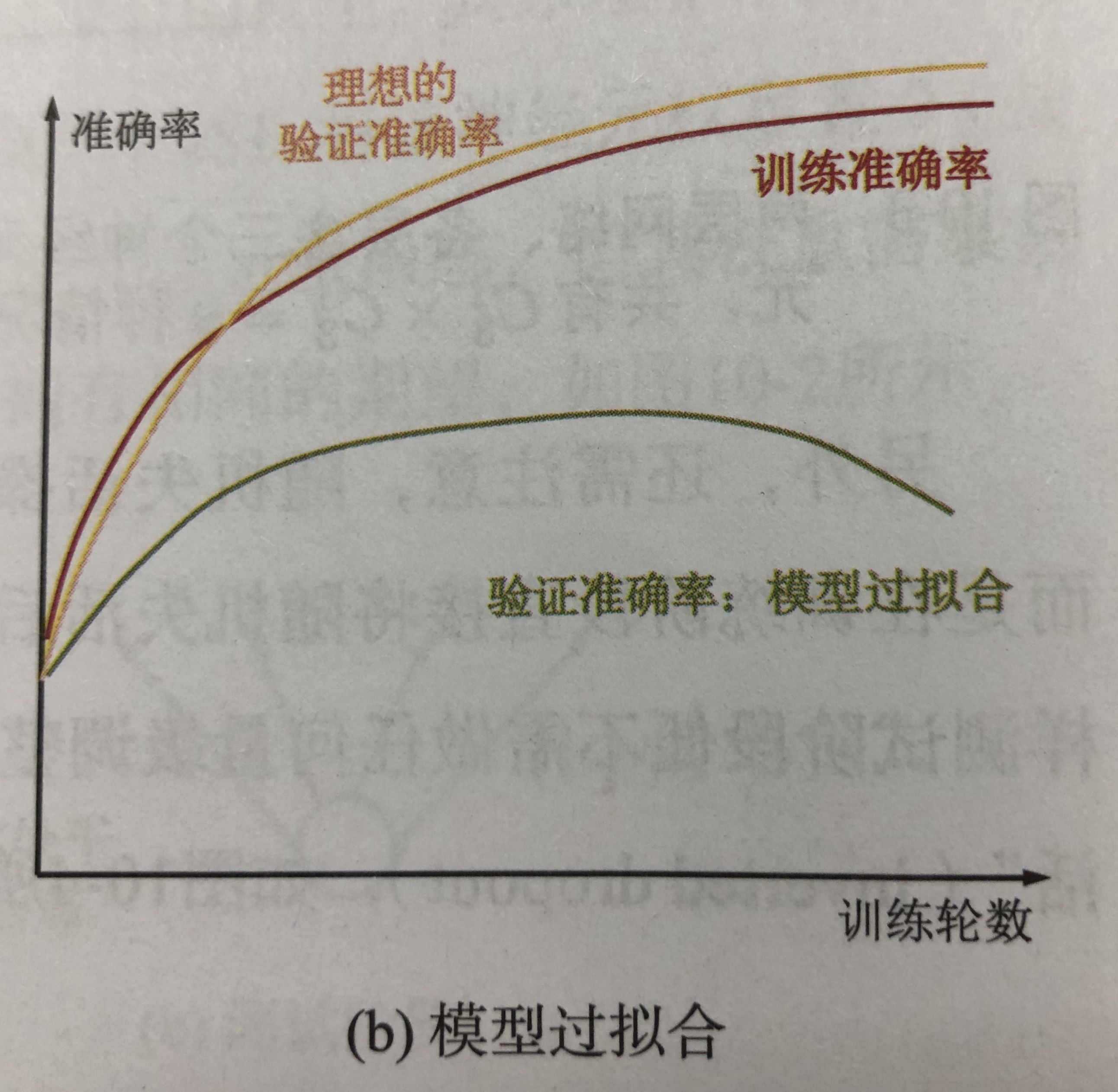

八  正负样本

    在分类问题中，正样本就是任务所要检测的目标物；负样本的选取与场景有关，不能是与你要研究的问题毫不相关的乱七八糟的场景图片，这样的负样本并没有意义。比如，如果你要进行教室中学生的人脸识别，那么负样本就是教室的窗子、墙等等。
    检测问题中的正负样本并非人工标注的那些框框，而是程序中（网络）生成出来的框框，也就是faster rcnn中的anchor boxes以及SSD中在不同分辨率的feature map中的默认框，这些框中的一部分被选为正样本，一部分被选为负样本，另外一部分被当作背景或者不参与运算。不同的框架有不同的策略，大致都是根据IoU的值，选取个阈值范围进行判定，在训练的过程中还需要注意均衡正负样本之间的比例。

8.2IoU（Intersection over Union）

    IoU的全称为交并比,作为目标检测算法性能mAP计算的一个非常重要的函数。如图，IoU计算的是“预测的边框”和“真实的边框”的交集和并集的比值。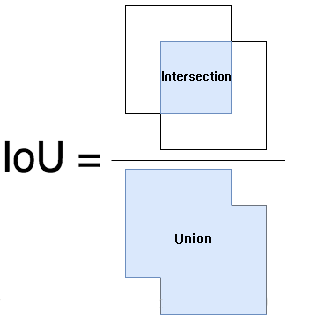

    我们使用loU看检测是否正确需要设定一个阈值，最常用的阈值是0.5，即如果loU>0.5，则认为是真实的检测(true detection)，否则认为是错误的检测(false detection)。

8.2  MAP（Mean Average Precision）

    均值平均精度(Mean Average Precision)特别适用于我们预测目标与类的位置的算法。同时均值平均值对于评估模型定位性能、目标监测模型性能和分割模型性能都是有用的。
    MAP=所有类别的平均精度求和除以所有类别，即数据集中所有类的平均精度的平均值。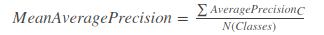

    参考：https://www.cnblogs.com/zongfa/p/9783972.html
    使用MAP值时我们需要满足一下条件：

• MAP总是在固定的数据集上计算。
• 它不是量化模型输出的绝对度量，但是是一个比较好的相对度量。当我们在流行的公共数据集上计算这个度量时，这个度量可以很容易的用来比较不同目标检测方法。
• 据训练中类的分布情况，平均精度值可能会因为某些类别(具有良好的训练数据)非常高(对于具有较少或较差数据的类别)而言非常低。所以我们需要MAP可能是适中的，但是模型可能对于某些类非常好，对于某些类非常不好。因此建议在分析模型结果的同时查看个各类的平均精度，这些值也可以作为我们是不是需要添加更多训练样本的一个依据。